Math

See also statistics, Linear algebra, and Computer science.

Logic

https://en.wikipedia.org/wiki/Reason#Logical_reasoning_methods_and_argumentation

Inductive
Deductive
https://en.wikipedia.org/wiki/Na%C3%AFve_physics
https://en.wikipedia.org/wiki/Folk_psychology
1945. How to Solve It by George Polya.
1954. Mathematics and Plausible Reasoning by George Polya.

A language consists of:

Logical constants have the same meaning in all interpretations:
- true, false
- Connectives: negation, disjunction, conjunction, implication, equivalence
- Quantifiers: universal quantifier ∀ and existential quantifier ∃
- True equality
The domain or universe of discourse is a set, such as the natural numbers or real numbers.
Non-logical symbols: relation symbols or predicates like < or subset, function symbols like + or x, variable or constant symbols which take a single value in the domain. The signature specifies the arity of each function or relation.

Term logic or traditional logic by Aristotle.

350 BC. Prior Analytics is the first formal study of logic.
An argument is a series of true or false statements which lead to a true or false conclusion.
A syllogism is an argument with at least two premises, where one term is the subject of one premise and the predicate of another.
A term is a category or class with no inherent truth value.
A categorical sentence is a proposition which connects two terms, a subject and a predicate, with four possible verbs. Must be true or false (bivalent).
- belongs to every (a)
- belongs to no (e)
- belongs to some (i)
- does not belong to some (o)
- For Aristotle, a singular term is primary substance, which can only be a logical subject, that is, it can only be predicated of itself, (this) Socrates. It makes no sense to say every Socrates. Thus terms must always be universal.
- Problem of multiple generality: term logic fails to describe some valid inferences.
300 BC. Stoic logic has the unit of a proposition rather than terms, but had little impact.
https://en.wikipedia.org/wiki/Template:Aristotelian_logic

Classical logic

By Frege: Begriffsschrift (“concept-script”, 1879), Function and Concept (1891). Extends term logic and makes it more precise, with variables and quantifiers. Notion of a logical function which evaluates to true or false, and which can be used as inputs to other logical functions.
Laws of thought (Boole, 1854)
- law of identity (ID)
- law of excluded middle (EM: P ∨ ¬P). Equivalent to proof by contradiction. See also proof by exhaustion or casework.
- Law of noncontradiction (NC), explosion, or bivalence ¬(P ∧ ¬P). Independent of excluded middle.
Structural rule is an inference rule that operates on the sequent directly, not on a logical connective
- Exchange or permutation, or equivalently each side is a multiset.
- Idempotency of entailment obeys contraction or factoring. Allows viewing each side as a set.
- Monotonicity of entailment obeys the weakening rule: if a sentence follows deductively from a given set of sentences then it also follows deductively from any superset of those sentences. (A -> C) -> (A, B -> C).
- Cut rule: (A ⊢ X, B) and (C, X ⊢ D) -> (A, B ⊢ C, D)
Rules of replacement are logical equivalences that can apply to a subexpression
- Exportation: ((p ∧ q) → r) → (p → (q → r))
- contrapositive: (p → q) → (¬q → ¬p)
- de Morgan’s laws: ¬(p∧q)↔︎(¬p∨¬q) and ¬(p∨q)↔︎(¬p∧¬q)
- material implication: (p → q) → (¬p ∨ q)
Rules of inference apply to a whole expression
- Implication introduction
- Modus ponens or implication elimination: P → Q, P ⊢ Q.
  - Conditional proof.
- Conjunction introduction/elimination: (P, Q) → P ∧ Q
- Absorption: (P → Q) → (P → (P → Q))
- Modus tollens: (P → Q) → (¬Q → ¬P).

Structural proof theory by Gerhard Gentzen studies systems for analytic proof, which are in normal form and have semantic properties are exposed.

A proof calculus or proof system includes a formal language, axioms, and inference rules for line-by-line arguments.
Natural deduction has richer inference rules.
- Analytic proofs have no formula occurrence in both the principal premise of an elimination rule and the conclusion of an introduction rule.
Sequent calculus: every line is a sequent inferred from earlier lines.
- A sequent is a conditional assertion A_i ⊢ B_i for conditions A_i and consequents B_i. Here the turnstile ⊢, left conjunction, and right disjunction are structural operators.
- Analytic proofs are the normal forms. Related to decision complexity.
- 1934. Cut-elimination theorem: any proof using the cut rule can be transformed into a proof not using the cut rule.
Deep inference allows unbounded structural complexity.
- Calculus of structures allows upwards and downwards inference.

Non-classical logic

Intuitionistic logic requires constructive proofs, which are mathematical objects. Rejects the law of the excluded middle, double negation elimination.
1917. Lukasiewicz develops three-valued propositional calculus, the first non-classical logic.
Fuzzy logic
Quantum logic lacks a material conditional or material implication.
- 1968. Is Logic Empirical? by Hilary Putnam.
Substructural logic rejects a structural rule.
- Non-monotonic logic capture defeasible inferences with tentative conclusions, allowing belief revision, reasoning by default (due to lack of contrary evidence), and abductive reasoning (most likely explanations).
  - Relevance logic requires antecedent and consequent to be related.
- 1987. Linear logic is non-idempotent and contains quantum logic. By Jean-Yves Girard.
Modal logic uses necessarily ◻ and possibly ◊ logical constants.
- Method of analytic tableaux is the main proof procedure, which uses the analytic cut rule.

Propositional logic does not have variables or quantifiers. Also known as boolean logic or zeroth-order logic. Equivalent to Boolean algebra (1854).

Propositions can be true or false.
Logical connectives create compound propositions.
A literal is positive (a variable) or negative (negation of a variable).
A clause is a literal or disjunction of literals.
- A Horn clause has at most one positive literal.
  - A goal clause has no positive literals.
  - A definite clause has exactly one positive literal.
    - A fact is a variable.

First-order logic or predicate logic has quantifiers over natural numbers, but not sets or functions of natural numbers.

A term is a variable or function.
A formula is a predicate, negation of a formula, equality (p = q) or connective (p → q), or quantification (∀x p).

Second-order logic allows quantification over relation variables.

First-order logic

Model theory. An interpretation provides formal semantics for a language, that is, a relation $R^\mathcal M \subseteq M^n$ for each relation symbol R of arity n in a domain M.

A tautology is true in every possible interpretation.
A model is a specific interpretation. A structure is an arbitrary interpretation.
Complete model: every valid sentence can be proven from the formal axioms.
Compact model: if every finite subset of a set of sentences has a model, then the entire set has a model.

A theory is a set of sentences or axioms. A theory is satisfiable if there exists a model which satisfies all its sentences. A theory is valid if it’s true in all possible models.

Gödel’s Completeness Theorem: first-order logic is complete i.e. all true statements are provable (in countable steps).

Zermelo-Fraenkel set theory

ZFC with the axiom of choice.
Language is first-order logic, avoiding Russell’s paradox.
No ur-elements, a member of a set that is not itself a set.
Axiom of extensionality: sets A and B are equal iff they have the same elements: ∀X, X∈A↔︎X∈B → A=B.
Axiom of pairing: For any objects A and B, there exists a set C whose members are exactly A and B. Formally, ∀X, X∈C ↔︎ X=A∨X=B.
A well-founded relation is a binary relation R on a set X where every non-empty subset S has a minimal element m. For example, < is well-founded.
- A minimal element means that R(s, m) is false for every s∈S.
- A set is well-founded if there is no infinite descending membership sequence.
Axiom of regularity: every non-empty set A contains an element X∈A that is dijoint from A (X ∩ A = ø).
- With pairing, this implies that no set is an element of itself, and there is no infinite sequence where each element is a member of its precedessor.
- Implies well-founded sets or set induction.

A well-ordered set is a total ordering such that every non-empty subset has a least element.

Two well-orders are order isomorphic if there is a correspondence between elements of the two sets so that the orders are the same.
The well-ordering principle (WOP) is equivalent to the axiom of choice.
WOP allows proof by infinite descent: if a statement holds for a number, it would hold for a smaller number.
Transfinite induction operates on well-ordered sets, such as sets of ordinal numbers or cardinal numbers.

Self-reference

Abstraction or self-reference lead to contradiction.

Liar’s paradox: “this statement is false” occurs in languages where we can correlate statements and predicates on statements.

600 BC. Epimenides paradox: a Cretan says “all Cretans are liars”.

1901. Russell’s paradox: naive set theory and any set theory that contains an unrestricted comprehension principle is inconsistent. Unrestricted comprehension means that it is possible to define all objects with a property. We can define the set S = {x | x not in x} and ask whether S contains itself. S in S iff S not in S, a contradiction. Part of The Principles of Mathematics (1903).

1905. Poincaré and Russell suggest the vicious circle principle to ensure predicativity.
- An impredicative definition invokes, mentions, or quantifies over the set being defined (usually indirectly, via another set that contains the new set).
- Stratified or ramified theories ensure predicativity by tracking levels of quantification.
A class is a collection of sets that can be defined by a property that all its members share. A proper class is not a set.

1910. Principia Mathematica by Alfred Whitehead and Bertrand Russell on mathematical logic. It develops a logical foundation for mathematics that resolves Russell’s paradox using a type theory.

1937. New Foundations by Willard Quine is a set theory related to the type theory of Principia Mathematica, where the Axiom of Choice is false. Non-well-founded.

1929. Gödel’s completeness theorem: first-order logic is complete, i.e. all true statements are provable.

1931. Gödel’s first incompleteness theorem. a complete and consistent set of axioms for arithmetic is impossible. Robinson arithmetic is incomplete, i.e. it contains statements which can neither be proved nor disproved, because it can express the Gödel sentence (“this sentence is unprovable”) or the halting problem. Each symbol and well-formed formula can be encoded as a Gödel number, a unique natural number.

Gödel’s second incompleteness theorem. A formal system F containing Robinson arithmetic can express the formula consistent(F) or Con(F) = “there does not exist a natural number coding a formal derivation within the system whose conclusion is a syntactic contradiction”. By diagonalization, Con(F) is not provable in F.
No consistent theory T that contains Robinson arithmetic Q can interpret Q + Con(T), the statement that T is consistent. However, Con(T) can be proven in a stronger theory.

Tarski’s undefinability theorem says that arithmetical truth cannot be defined in arithmetic.

Cantor’s diagonal argument shows that the real numbers are uncountable.
Cantor’s theorem states that the power set of S is larger than S. Consider a map f which associates each member x of S with a subset of S. Can f cover all the subsets of S? No: there is no y s.t. f(y) = {x | x not in f(x)}. Otherwise, y in f(y) iff y not in f(y), a contradiction. This argument applies more generally any time we objects of a domain are attached to predicates over the same domain. Then we can apply to an object the predicate that it represents.

Cardinal numbers represent the size of a set. The first infinite cardinal number is ℵ_0, the cardinality of the natural numbers.

The continuum hypothesis states that there is no cardinal number between ℵ_0 and the cardinality of the real numbers (continuum) ℵ_1.
1897. Burali-Forti paradox shows that there is no largest ordinal number, and no set of all ordinal numbers.
1899. Cantor’s paradox states that there is no largest cardinal number, and no set of all cardinalities.

Ordinal numbers represent an order isomorphism class or a location in a well-ordering. von Neuman ordinals are a canonical representation that defines an ordinal as the set of ordinals that precede it. The smallest infinite ordinal is ω, the natural numbers. Ordinals have addition, multiplication, and exponentiation.

Burali-Forti paradox shows that the class of all ordinal numbers is proper.
Surreal numbers and hyperreal numbers extend the reals.

Ordinal analysis. A theory can prove transfinite induction for well-orders up to its proof-theoretic ordinal.

Robinson arithmetic has ordinal ω.
Peano arithmetic has ordinal ε_0. ε_0 is the limit of ω, ω^ω, ω^ωω, … or the smallest ordinal such that ε_0 = ω^ε_0. ε_1 is the limit of ω^(ε_0+1), ω^ω(ε_0+1), …
- Gentzen’s consistency proof shows that the Peano axioms of first-order arithmetic are consistent if primitive recursive arithmetic with the additional principle of quantifier-free transfinite induction up to ε_0 is consistent.
Reverse mathematics defines the subsystems of second-order arithmetic needed to prove various statements.
- Recursive comprehension axiom RCA_0 or constructive mathematics has ordinal ω^ω.
- Weak Kőnig’s lemma WKL_0 or Hilbert’s finitistic reductionism has ordinal ω^ω.
- Arithmetical comprehension axiom ACA_0 has ordinal ε_0.
- Arithmetical transfinite recursion ATR_0 has ordinal Feferman–Schütte ordinal Γ_0, the smallest ordinal such that Veblen function φ_Γ(0) = Γ.
- Π_1^1 comprehension axiom Π_1^1-CA_0 has ordinal Ψ_0(Ω_ω).

Halting problem: determining whether a program halt or run forever is undecidable. The program halts(f) cannot be total (defined for all programs), since then g := if halts(g): loop_forever leads to a contradiction.

Turing degrees are classes of Turing equivalent problems. There are problems harder than the halting problem because the halting problem relativizes. There is an undecidable problem that is weaker than the halting problem.

https://en.wikipedia.org/wiki/Paradox

Optical illusion

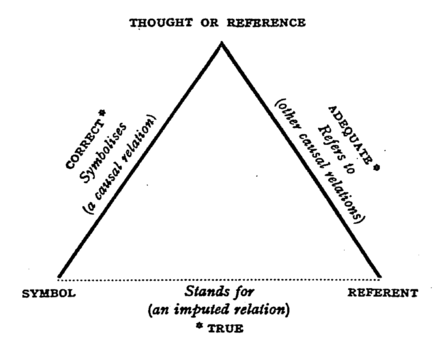
Linguistic dialectic

Semiotics, the study of reference and sign relations, distinguishes between the signified (the meaning or idea that a sign evokes) and the referent (the actual thing a sign refers to).
The extension of a concept, idea, or sign consists of the things to which it applies. Often a tautology.
The intension of a word or phrase is the properties implied by the concept. The comprehension of an object is the totality of its intensions. Natural language is intensional.
An intensional statement involves operators like “believes”, “is happy that”, “is possible that”, “character length of”.
- Lois believes Clark Kent is weaker than Superman. De re (“about the thing”), this is a contradiction. De dicto (“about what is said”), this is a reasonable belief.
- In an opaque context, it is not always possible to substitute co-referential expressions.
- 400 BC. Masked-man fallacy by Eubulides: “Do you know this masked man?” “No.” “But he is your father. Thus, you not know your own father.”
- Intensional contexts violate the disquotational principle, that a person will accept “p” iff they believe p.
Use-mention distinction
- Map-territory relation
- Sense and reference
- A white horse is not a horse 白马非马 by Gongsun Long, 250 BC.
Fuzzy concept is applicable “to an extent”.
- Sorites paradox by Eubulides.
Presupposition
- Horns paradox: What you have not lost, you have. But you have not lost horns. Therefore, you have horns.
1892. Frege writes On Sense and Reference on analytic philosophy of language
1960. W. V. Quine writes Word and Object on the inscrutability of reference.
1965. Aberrant decoding by Umberto Eco.

Elementary algebra

L1 norm

Diamond-shaped contours = more likely that a solution lies on a coordinate axis. Norm grows more slowly around zero, so it shrinks smaller coefficients toward zero more aggressively.
Non-differentiable = harder to optimize
Equivalent to a Laplacian prior, which has a sharp peak at 0.
Compressed sensing reconstructs a sparse signal which has a small number of nonzero coefficients.
Basis pursuit minimizes $\|x\|_1$ s.t. $y=Ax$.

Vieta’s formulas: normalizing a polynomial to leading coefficient 1, the coefficients are the elementary symmetric polynomials of the roots.

the second coefficient is the negative sum of the roots
the last coefficient is the (possibly negative) product of the roots.
Vieta jumping (IMO 1988)

Combinatorics

Pascal’s identity. $\displaystyle\binom{n-1}k+\binom{n-1}{k-1} = \binom{n}k$, pick $n$ elements including or excluding $x$

Hockey-stick identity. $\displaystyle\sum_{i=r}^n\binom{i}r = \binom{n+1}{r+1}$

There are $\binom{n-1}{r-1}$ ways to distribute $n$ indistinguishable balls into $r$ distinguishable boxes s.t. each box contains at least one ball.
There are $\binom{n+m}n$ arrangements of $n$ black and $m$ white balls.

Flip $k$ coins with $P(\text{heads})=p$. Expect $1 + 2(k-1)p(1-p)$ runs because transition probability is $2p(1-p)$. Expect $p+(k-1)p(1-p)$ runs of heads.
$\V[R] = \E[R^2]-\E[R]^2$, where $\E[R^2] = \sum\sum \E[t_it_j]$ can be computed by breaking into 3 cases:

$i=j$, $\E[t_i^2] = \E[t_i]$, total is just $\E[R)$.
$|i-j|=1$: one must be 0 so product is 0.
$|i-j|>1\Rightarrow$ independent, just need to account for whether one is the first coin.

Arrange $n$ black and $m$ white balls uniformly at random. For $r$ black runs and $s$ white runs,
$\displaystyle P(r, s)=\frac{\binom{n-1}{r-1}\binom{m-1}{s-1}}{\binom{n+m}n}\times \begin{cases} 1,&|r-s|=1\\ 2,&r=s\\ 0,&\text{else} \end{cases}$

$\displaystyle P(r) = P(r,r\pm1)+P(r,r) = \frac{\binom{n-1}{r-1}\left[\binom{m-1}{r-2}+2\binom{m-1}{r-1}+\binom{m-1}r\right]}{\binom{n+m}n}=\frac{\binom{n-1}{r-1}\binom{m+1}r}{\binom{n+m}n}$

$\displaystyle E(r) = \sum_{r=0}^n \frac{r\binom{n-1}{r-1}\binom{m+1}r}{\binom{n+m}n} = \frac{m+1}{\binom{n+m}n}\sum_{r=0}^n \binom{m}{r-1} \binom{n-1}{r-1} = \frac{m+1}{\binom{n+m}n}\binom{m+n-1}m = \frac{(m+1)n}{m+n}$

$\displaystyle V(r) = E(r^2) - E(r)^2 = \frac{n(m+1)(mn+n-1)}{(m+n)(m+n-1)} - E(r)^2 = \frac{(m+1)n}{m+n}\cdot\frac{m(n-1)}{m+n-1}$

Graph theory

https://en.wikipedia.org/wiki/List_of_graph_theory_topics

Hamiltonian path visits each vertex exactly once.
Eulerian path visits every edge exactly once
- 1736. Seven Bridges of Koenigsberg has no Eulerian path.
- Five-room puzzle has no Eulerian path.
- Euler’s theorem: an Euler cycle exists iff all vertices have even degree.
- 1912. Veblen’s theorem: edegs can be written as a union of disjoint simple cycles iff every vertex has even degree.
An induced subgraph is a subset of the vertices with all edges between them.
A hereditary property such as bipartite is true for all induced subgraphs.
Odd cycle transversal is a part of any odd cycle, so removing it induces a bipartite graph.
A matching or independent edge set has no common vertices.
- A perfect matching includes all vertices.
- In a factor-critical graph, every induced subgraph of n − 1 vertices has a perfect matching.

https://en.wikipedia.org/wiki/Transportation_theory_(mathematics)

A cut partitions the vertices into two disjoint subsets.
- https://en.wikipedia.org/wiki/Maximum_cut
- Minimum k-cut: smallest edge set that creates at least k connected components when removed.
  - Karger’s algorithm
- A bridge is an edge which increases the number of connected components when deleted.
A k-connected graph remains connected after removing fewer than k edges.
- A bridge is an edge which can
A flow network or transportation network is a directed graph where each edge has a flow and a capacity. The source only has flow out, the sink only has flow in, and all other nodes must have equal flow in and out.
Maximum flow = min cut (duality)
- LP: define flow function over edges (pipes) s.t. capacity and conservation constraints
Minimum-cost flow problem
Ford-Fulkerson: repeatedly add augmenting path in residual network. An augmenting path is an available flow from source to sink. The bottleneck is the minimum residual capacity in an augmenting path.
- bfs to find aug path is Edmonds-Karp

Handshaking lemma: there is an even number of people who shake hands with an odd number of people.

Routing problems

Travelling salesman problem (TSP): NP-complete, but can easily be approximated within 1%.
Vehicle routing problem: delivery routes for a fleet of vehicles.
Vehicle rescheduling problem: how to handle a breakdown or delay.
Canadian traveller problem or Stochastic Shortest Path Problem with Recourse is partially observable.
Traveling purchaser problem: route a shopping list given list of marketplaces and their prices.
Chinese postman problem: min cost Eulerian tour, which vists each edge at least oncec. O(V^3)
- Mixed CPP: graph has both directed and undirected edges. NP-complete.
Dead mileage or empty legs: commercial vehicle runs without revenue passengers
- Deadheading: airline and train crews can ride free of charge.
- Jump seat is a folding auxiliary seat.
Longest path problem: NP-complete in general.

https://en.wikipedia.org/wiki/Template:Covering/packing-problem_pairs

Vertex cover: smallest vertex set that touches every edge.
- Vertex cover of size k on a graph of size n can be found in O(2^k n). Keep every vertex of degree k or more. If more than k^2 edges remain, then the cover is infeasible, so feasible solutions can be solved by brute force.
Assignment problem: bipartite graph matching
- https://en.wikipedia.org/wiki/Matching_pursuit
Nurse scheduling problem for employee schedules with constraints
https://en.wikipedia.org/wiki/Activity_selection_problem
https://en.wikipedia.org/wiki/Assignment_problem#See_also

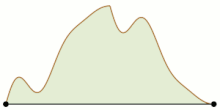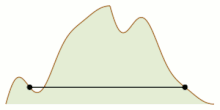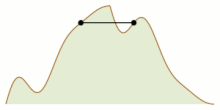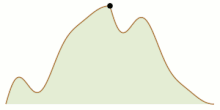
Mountain climbing problem: two mountain climbers starting at sea level on opposite sides can meet at the summit while maintaing equal altitude at all times.

Combinatorial math

Ramsey’s theorem: every blue-red edge coloring of the complete graph on R(r, s) vertices contains a blue clique on r vertices or a red clique on s vertices.
Four color theorem: four colors are sufficient to color a map such that no adjacent regions have the same color. The chromatic number of a loopless planar graph is 4.
Apollonian network: undirected graph formed by recursively subdividing a triangle into three smaller triangles.
Collatz conjecture: the Collatz function f(n) = 3n+1 if n is odd else n/2 always iterates to 1.
- “Mathematics may not be ready for such problems.” -Erdos
https://en.wikipedia.org/wiki/Addition_chain

Geometry

Pons asinorum (“bridge of asses”): an isosceles triangle has two equal angles.

Fermat point is geometric median

Trigonometry

cos x = Re(exp ix) = (exp ix + exp(-ix))/2
sin x = Im(exp ix) = (exp ix - exp(-ix))/(2i)

cos x cos y = (cos(x+y) + cos(x-y))/2
cos nx = cos((n-1)x) (2 cos x) - cos((n-2)x)
Integral can be computed using Euler’s identity. E.g. ∫ cos^2(x) = 1/4 (2x + sin 2x) + C.

Curvature is the second derivative, or the reciprocal of the radius of an osculating circle tangent to the smooth curve.
An inflection point is a change in curvature.

An evolute is the locus of all its centers of curvature. Extreme points of curvature form cusps on the evolute.

Descartes’ theorem relates the curvatures of four kissing (mutually tangent) circles: (sum c_i)^2 = 2 sum c_i^2.

Apollonian gasket: mutually tangent circles.

Four-vertex theorem: the curvature along a simple, closed, smooth plane curve has at least two local maxima and at least two local minima.

A monostatic polytope can stand on only one face.
A gömböc has one stable and one unstable equilibrium point.
curve of constant width: Reuleaux triangle

Tennis ball theorem theorem: a smooth curve that divides a ball into two equal-area subsets without touching or crossing itself must have at least four inflection points.

Non-Euclidean geometry

A projective space is a space with a point at infinity for each direction.

projective transformations do not preserve angles.
Incidence geometry studies projective planes, where any two points lie on a unique line and any two lines meet at a unique point.
- The Fano plane is the smallest finite projective plane.
- In a configuration, each point is incident to the same number of lines and each line is incident to the same number of points.

https://en.wikipedia.org/wiki/Template:Tessellation

Voronoi diagram: given a set of points, find the area closest to each point.
- Fortune’s algorithm

Abstract algebra

An equivalence relation is reflexive, symmetric, and transitive.
Equivalence relations partition elements into disjoint equivalence classes.

Category theory. A category is a collection of objects linked by composable morphisms or arrows, where the identity arrow exists for every object.

A functor is a mapping between categories. First studied in algebraic topology.
An endomorphism is a map from a set to itself.
An isomorphism is a reversible morphism.
An automorphism is an isomorphic endomorphism.

A magma is a set with a closed binary operation.
A semigroup is an associative magma.
A monoid is a semigroup with identity.

A universal property characterizes objects up to isomorphism, independently of the choice of construction.

Universal algebra studies algebraic structures themselves, not examples (“models”) of structures. E.g. the class of groups.
A free object over a set A is a “generic” algebraic structure over A.
- A word is any written product of group elements and their inverses.
- A free group over S contains all words that can be generated from S.
- A variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities.

A group is a set with an associative operation that has an identity and an inverse. An abelian group is commutative.

An abstract group is defined by a presentation consisting of a set of generators and relations on the generators. The cyclic group of order n has the presentation a^n = 1.
A subgroup H of G partitions of G into equal-size subsets known as cosets, which are translates of H. For a fixed g, the left coset gH = $\{ g+h | h\in H \}$.
The index G : H is the number of left cosets of H in G.
Lagrange’s theorem states that |G| = |G : H| |H|. The order of any subgroup divides the order of the group.
- $g^{|G|} = 1$.
- Fermat’s little theorem. For prime $p$, $a^p = a \pmod p$.
- Euler’s theorem states that if $n$ and $a$ are coprime, then $a^{\phi(n)} = 1\ mod\ n$, where Euler’s totient function $\phi(n)$ counts the numbers between 1 and n inclusive that are coprime to $n$. Relevant for RSA encryption.
The order or period of an element is the order of the subgroup generated by the element or equivalently the smallest positive $k$ where $a^k = 1$.
- A primitive root has order phi(n), or p-1 for prime p.
- The order of a bth residue divides phi(n)/2. Proof. Suppose a is a bth residue: a = x^b mod p. x^phi(n) = 1, so a^(phi(n)/b) = x^phi(n) = 1, so the order of a divides phi(n)/b.
  - As a corollary, every primitive root is a nonresidue.
  - For example, since 2 is a quadratic residue and a fifth order residue of 641, 2^64 = 1 mod 641. Further, 2^32 != 1 mod 641 since 2 is not a quartic residue. Thus, 2^32 + 1 is divisible by 641.
- The period of the decimal expansion of 1/n is the multiplicative order of 10 mod n.
The group action of G on some set X is a group homomorphism from G to a group (under function composition) of transformations from X to itself.
- The orbit of x $Gx = \{gx | g\in G\}$. The set of orbits X / G partitions G.
- The stabilizer of x $G_x = \{g | gx = x\}$. If $y = gx$, then $G_y = g G_x g^{-1}$. $X^g$ is the set of points fixed by g.
- Orbit-stabilizer theorem. |Gx| |G_x| = |G|.
- Burnside’s lemma or orbit counting lemma. $|X / G| = \frac1{|G|} \sum |X^g|$.
- Polya enumeration theorem
An inner automorphism is the conjugation action $y = g^{-1} x g$. x and y are conjugates, which is an equivalence relation.
- The center Z(G) is the set of elements that commute with every element.
- Class equation. |G| = |Z(G)| + the sizes of its nontrivial conjugacy classes.
A normal subgroup N is invariant under conjugation by its elements or equivalently if $gN = Ng$ for all g.
A quotient group is a group structure over equivalence classes of a larger group. Given a normal subgroup N, the quotient group $G / N = \{ gN | g\in G \}$, the set of left cosets.
A characteristic subgroup is mapped to itself by every automorphism of the group. Every characteristic subgroup is normal since conjugation is an automorphism.
A simple group has no nontrivial subgroups. The only simple abelian groups are the cyclic groups of prime order. Every finite simple group is cyclic, alternating, one of 16 families of groups of Lie type, or one of 26 sporadic groups.
- The monster group is the largest sporadic group, of order around 10^53, and is the automorphism group of the monster vertex algebra, which is related to the j function, a modular function.

Representation theory studies abstract algebraic structures by describing its elements as linear transformations of modules.

Modules generalize vector spaces by replacing the field of scalars with a ring. An abelian group is a module over the ring of integers.
Group representations describe abstract groups in terms of bijective linear transformations of a vector space to itself.
- Group elements can be represented as invertible matrices.
- Group operation can be represented as matrix multiplication.

A lattice is a partially ordered set (poset) in which every pair of elements has a unique supremum (least upper bound or join ∨) and infimum (meet ∧).

Rings

A ring has addition and associative distributive multiplication.

Integers Z is a ring. Can be defined as N with all additive inverses.
Abelian group under addition.
No need to be commutative.
Commutable ring and commutable algebra: no need to be invertible. Integers and square matrices.
An ideal is an additive subgroup that absorbs multiplication by elements of R: for all r ∈ R and x ∈ I, rx ∈ I.
- A principal ideal is generated by one element of R via multiplication by all elements.
- For the integers, every ideal is a principal ideal consisting of the multiples of a positive integer.
Frobenius endomorphism is a special endomorphism of commutative rings with prime characteristic p, an important class that includes finite fields. The endomorphism maps every element to its p-th power.
An integral domain is a nonzero commutative ring in which the product of any two nonzero elements is nonzero. Every nonzero element has the cancellation property that if a != 0, ab=ac implies b=c. It generalizes the integers.
Euclid’s lemma says that if a prime p divides ab, then p divides a or b.
The fundamental theorem of arithmetic states that every integer has a unique prime factorization.
A unique factorization domain is an integral domain where the fundamental theorem of arithmetic holds.
Polynomial ring is the set of polynomials with coefficients from a field.

A field is a ring where multiplication is commutative and invertible.

An ordered field has a total order consistent with addition and multiplication.
The rational numbers are an ordered field. Can be defined as Z with multiplicative inverses. Countable.
Finite field: residues modulo a prime p are a field.
Galois theory studies symmetries of field extensions.

A prime cannot be expressed as the product of two non-units.

Number theory

Natural numbers N are discrete and ordered. Set of zero and its successors.

Pigeonhole principle. If n items are put into m containers, with n > m, then at least one container must have multiple items.

Numeral system

Hindu-Arabic numerals are positional.
Tally marks and Roman numerals: numerals largely represent the same amount regardless of position (sign-value notation)

Gaussian integers are a + bi, with units 1, -1, i, and -i. A positive integer is a Gaussian prime if it is a prime that is 3 mod 4. The norm of a Gaussian integer is its product with its conjugate, and is multiplicative. Gaussian integers form a principal ideal domain.

Extended Euclidean algorithm produces the Bézout coefficients x and y satisfying ax + by = gcd(a,b).

a^(-1) mod m only exists if a and m are coprime, in which case we can compute x satisfying ax + my = gcd(a, m) = 1.
Chinese remainder theorem solves x = a (mod m) and x = b (mod n) for coprime m and n. x = adn + bcm is a solution, where cm + dn = 1.
- Residue number system represents integers by their numbers modulo several coprime integers.

$a$ is a quadratic residue mod $n$ if $x^2 = a \pmod n$ for some $x$.

A nonzero polynomial over a field has at most as many roots as its degree. Lagrange’s theorem states that a nonzero polynomial of degree n over ℤ/pℤ has at most n roots. In particular, $x^2 = a \pmod p$ has at most two solutions, so there are at least (p-1)/2 distinct quadratic residues modulo p.

The Legendre symbol $\left(\frac{a}{p}\right) = \begin{cases} 1 & \text{if } a \text{ is a quadratic residue}\\ -1 & \text{if } a \text{ is a quadratic nonresidue} \\ 0 & \text{if } p | a \end{cases}$ for an odd prime p.

Euler’s criterion: $\left(\frac{a}{p}\right) \equiv a^{\tfrac{p-1}{2}} \pmod p$.
In particular, -1 is a quadratic residue iff p = 1 mod 4.
By Fermat’s little theorem, $2^{p-1} = 2^{8k} = 1\pmod p$.
Proof: $a^p = a \pmod p$ can be written as $\left( a^{\tfrac{p-1}{2}}-1 \right)\left( a^{\tfrac{p-1}{2}}+1 \right) \equiv 0 \pmod p,$ one of which must be 0. Every quadratic residue makes the first factor 0, and by Lagrange’s theorem, there can only be (p-1)/2 solutions for the first factor, so the nonresidues must make the second factor 0.

Quadratic reciprocity relates solvability of x^2 = p mod q and x^2 = q mod p. $\left(\frac{p}{q}\right) \left(\frac{q}{p}\right) = (-1)^{\frac{p-1}{2}\frac{q-1}{2}}$.

The second supplement states that 2 is a quadratic residue iff p = 1 or -1 mod 8. Proof: for s = (p-1)/2, consider:
$1= (-1)(-1) \\ 2=2(-1)^2 \\ 3=(-3)(-1)^3 \\ 4=4 (-1)^4 \\ \ \,\cdots\\ s= (\pm s)(-1)^s.$
The negative odd numbers are just the other even numbers since 2s = -1 mod p and 2(s-1) = -3 mod p, so the right side contains all even numbers. Multiplying together, $s! = s! 2^s (-1)^{s(s+1)/2}$ so $2^s = (-1)^{(p^2-1)/8}$.
a is a bth power residue iff x^b - a splits into linear factors mod p.
2 is a quadratic residue iff p splits in Z[sqrt(2)] as a product of two primes. Class field theory says that a prime splits in an abelian extensions iff $\chi\colon (\mathbb Z/8\mathbb Z)^\times\to \mathbb C^\times$ has $\chi(p) = 1$.

Dirichlet’s theorem on quadratic residues

Quartic reciprocity. If p = 3 mod 4, then a is a quadratic residue mod p iff it is a quartic residue. Proof. -1 is a quadratic nonresidue mod p, so for any x, exactly one of x and -x is a quadratic residue. Thus if a quadratic residue a = x^2 mod p, either x = y^2 or -x = y^2.

Thus only p = 1 mod 4 is unsolved. -1 is a quartic residue iff p = 1 mod 8. 2 is a quadratic residue iff p = 1 mod 8, in which case we can express p = a^2 + 2b^2, and 2 is a quartic residue iff p = a^2 + 64b^2.

p-adic numbers.

Diophantine equations

Brahmagupta–Fibonacci identity or Diophantus identity. The set of sums of two squares is closed under multiplication.
Taxicab numbers are the smallest numbers expressible as a sum of n cubes in n different ways.
Fermat’s theorem on the sum of two squares: an odd prime p can be expressed as the sum of two squares iff p is 1 mod 4.

Euler’s four-square identity: the product of two sums of four squares is a sum of four squares.

Hurwitz’s theorem says a bilinear identity is only possible for n = 1, 2, 4, 8 (Degen’s eight-square identity). Pfister’s sixteen-square identity is non-bilinear.
Lagrange’s four-square theorem (1770): every number is the sum of four squares.
Fermat polygonal number theorem (1813): every positive integer is a sum of at most n n-gonal numbers.
Hilbert-Waring theorem (1909): every number k has an associated integer s such that every number is the sum of at most s numbers raised to the power of k.

Midy’s theorem.

Geometry of numbers

1889. Minkowski’s theorem: every convex set in R^n symmetric with respect to the origin with a volume greater than 2^n contains a nonzero integer point.

Linear algebra

Einstein notation sums over index variables that appear twice in a term. For example a dot product is a_i b^i. Free indices appear once per term and are not summed over.

Vectors are contravariant and use upper indices: v = e_i v^i. For example, changing from cm to m scales the basis vector by 100, and scales the vector components by 1/100.
Covectors or dual vectors are covariant row vectors and use lower indices: w = w_i e^i.
Invariant vectors, such as distance in Euclidean space, do not change when we change the coordinate system.

Jacobian matrix: $J_{ij} = ∂ f_i / ∂ x_j$ for $f(x): R^n \to R^m$.

For a vector space V over a field F, its dual space V* is the space of linear forms V -> F.

If elements of V are column vectors, then elements of V* are row vectors or covectors, which can be interpreted as linear maps or homomorphisms.
V* is also a vector space over F.
Vector spaces U and V are dual iff there is a nondegenerate bilinear map from U×V to F.
The dual space V* is dual because the natural pairing that maps (φ, x) to φ(x) is a nongenerate bilinear form.
Given a basis $\{e_i\}$ of V, there is a natural bi-orthogonal dual basis $\{f(x) = x_i\}$. The ith dual basis element maps a vector to its ith coordinate.
For a linear map f: V -> W, the dual or algebraic adjoint f* maps W* to V. For x in W, f* returns x∘f, the precomposition by f or pullback of x along f, which is an element of V*.
- If f is a matrix, then its dual is the matrix tranpose.

Vectors are contravariant: their numerical components vary inversely with a change of basis. If we divide a basis vector by 100 (changing from meters to centimeters), the vector components will multiply by 100 in the new basis.
Covectors are covariant: they transform in the same way as a change of basis.

Exterior algebra has a wedge product ∧ s.t. v ∧ v = 0 for all v. A k-blade is the wedge product of k vectors and is the directed hypervolume of the parallelotope. A bivector is a 2-blade.
A geometric algebra or Clifford algebra has an inner product.

Geometric product ab = a·b + a∧b.

Algebraic geometry

Algebraic geometry is the geometry of solutions to polynomial equations.

An algebraic variety is the space of solutions of a system of polynomial equations: conic sections, cubic curves like elliptic curves, quartic curves like lemniscates and Cassini ovals. A variety over a rational field has a finite number of rational points.

Affine variety in Euclidean space, versus projective variety.
- Every smooth complex projective variety is a Kähler manifold.
Coordinate rings are quotient rings constructed from polynomial rings modulo certain ideals.
subvariety is irreducible if it cannot be expressed as the union of two proper closed subvarieties. codimension of a closed subvariety is $\sup {n | \exists Z = Z_0 \subsetneq Z_1 \subsetneq ... \subsetneq Z_n \subseteq X \text{ irreducible closed } }$
dim(X) = sup{codim(Z,X)∣Z is a closed subvariety of X}.
dimension of an algebraic variety.
singularities like cusps. tools like blowing up resolve singularities.
topology: connectivity and fundamental groups.
Diophantine geometry studies rational points of varieties.
relatively weak Zariski topology.
An elliptic curve is the solutions to y^2 = x^3 + ax + b.
- The curve is nonsingular, with no cusps or self-intersections. It must be square-free in x <-> 4a^3 + 27b^2 != 0.$
- Elliptic curves over the complex numbers correspond to embeddings of the torus into the complex projective plane.
- The identity element is the point at infinity.

A scheme generalizes an algebraic variety. A scheme is glued from a sheaf of affine schemes just like manifolds are glued from pieces that resemble R^n.

It is a topological space that glues together spectra (spaces of prime ideals) of commutative rings along their open subsets. Introduced by Grothendieck.
Algebraic stacks generalize schemes.

A toposis a category that behaves like the category of sheaves of sets on a topological space.

étale cohomology groups of a scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space.
Weil conjectures concern local zeta functions, which are generating functions where the kth coefficient counts rational points on a variety over the the extension field with q^k elements. Weil conjectured that the local zetas are rational functions and shares some properties with the Riemann zeta function.
Finite geometry or discrete geometry
- Galois geometry studies algebraic geometry over a finite field or Galois field.
- Fano plane

1840. Dirichlet’s approximation theorem.
1844. Liouville numbers are transcendental.

E.g. the nth binary digit is 1 iff n = k! for integer k.
1933. Champernowne constant is transcendental and normal.

Prime-counting function π(n) is the number of primes less than or equal to n.

Bertrand’s postulate (1852): there is always a prime number between k and 2k.
Prime number theorem: π(n) approaches n / log n.
- Selberg’s identity estimates the log density of primes.
Green-Tao theorem (2004): the primes contain arbitrarily long arithmetic progressions.

Dirichlet series. sum a_n / n^s.
Riemann zeta function. ζ(s) = sum 1/n^s.

Zeros at -2, -4, … are trivial zeros.
Euler product formula: ζ(s) = sum over primes 1/(1-p^{-s})
All nontrivial zeros lie on the critical strip 0 < Re(s) < 1.
Riemann hypothesis: all nontrivial zeros lie on the critical line Re(s) = 1/2.

1967. Langlands program relates Galois groups in algebraic number theory to automorphic forms and algebraic groups over local fields. General analysis of invariance for algebraic structures and arithmetic objects through their automorphic functions.

1983. Fundamental lemma: direct connection between the generalized fundamental representation of a finite field with its group extension to the automorphic forms under which it is invariant. Accomplished via abstraction to higher dimensional integration, by an equivalence to a certain analytical group as an absolute extension of its algebra. This allows an analytical functional construction of powerful invariance transformations for a number field to its own algebraic structure. Proved by Ngo Bao Chau, 2010 Fields Medal.

Chaos theory: fractal self-similarity, Mandelbrot set, bifurcation theory, Lyapunov time.

https://news.ycombinator.com/item?id=39145513

Topology

Topology is the geometry of “rubber sheets”. It studies qualitative spatial properties invariant under continuous deformations like stretching without tearing or gluing.

A topology τ is defined as a collection of open sets, which describe spatial relations between members of a set X:

The empty set and X is in τ.
any union of members of τ is in τ.
any intersection of a finite number of members of τ is in τ.

A subset is closed if its complement is an open set.

A path is a continuous function from a closed interval onto X.

A connected space cannot be represented as the union of two disjoint open subsets.

A path-connected space has a path joining any two points.
A simply connected space has no holes.

A compact space can be covered by a finite number of open sets.

Separation axioms (“Trennungsaxiom”)

Two points are topologically distinguishable if they do not have exactly the same neighborhoods. There is an open set that one point belongs to and the other does not. One point does not belong to the other’s closure.
Two points are separated if each has a neighborhood that is not a neighborhood of the other. Neither belongs to the other’s closure.
In a Kolmogorov or T0 space, all distinct points are topologically distinguishable. Weakest separation axiom.
In a Hausdorff or T2 space, all distinct points have disjoint neighborhoods.

Algebraic topology finds algebraic invariants that classify topological spaces.

A homotopy is a continuous deformation.
Homotopy groups classify topological spaces.
The fundamental group of a topological space is the group of homotopy equivalence classes of loops in the space. First and simplest homotopy group. A space has a trivial fundamental group iff it has no holes.
A homeomorphism is an isomorphism between topological spaces. Continuous bijective function.
Homology is an equivalence class of holes (non-boundary cycles). A cycle is any closed manifold.
A cohomology is a sequence of abelian groups defined from a cochain complex. Algebraic dual of homology. It assigns algebraic invariants to a topological space that has a more refined algebraic structure than does homology.

Analysis

Real numbers R is continuous.

Dedekind complete: all supremums and infinums of all bounded sets of Q.
Complete metric space: every Cauchy sequence has a limit in the space.
Uncountable. Requires statements about collections. Nonfirstorderizable, not a first order logic theory. A statement with no first order logic formula which is true iff the statement is true.
Rationals are dense in the reals, and also a null set of the reals.

Functional analysis

Banach space is a complete normed vector space.
A Sobolev space is a space of functions with sufficiently many derivatives.

Complex numbers are algebraically closed.

Fundamental theorem of algebra: every nonconstant polynomial with complex coefficients has a complex root.
$i$ is the root of $x^2 + 1$.
Complex numbers represent rotations. Can be written in polar or exponential form.
Rotation property: $\exp(a+b) = (\exp a)(\exp b)$
$\exp i\theta = \cos\theta + i \sin\theta$
Complex log is multivalued: $\ln z = \ln|z| + i\theta$.

Convergence

Diverges if $\lim a_n \not\to 0$.
Alternating series: converges if $|a_n|$ decreases monotonically and $\lim a_n \to 0$.
Direct comparison test: converges if bounded by a convergent series, and diverges if it bounds a divergent series.
Limit comparison test: If $\lim a_n/b_n$ is constant, then either both converge or both diverge.
Ratio test: $\lim |a_{n+1} / a_n|$.
L’Hopital’s rule. $\lim_{x\to c}{\frac{f}{g}}=\lim_{x\to c}{\frac{f'}{g'}}$
1817. Intermediate value theorem

Differential

Linear
(x^n)’ = n x^(n-1)
Product rule. (uv)’ = u’v + uv’
Quotient rule. $h'=\frac {f'g-fg'}{g^2}$
Implicit differentiation.

A Taylor series or Taylor expansion of a function at $a$ is:
$f(a) + \frac {f'(a)}{1!} (x-a) + \frac {f''(a)}{2!} (x-a)^2 + \cdots$
$= \sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!} (x-a)^n$.

Known as a Maclaurin series when expanded at 0.
Taylor’s theorem: the k^th order Taylor approximation has error O(|x-a|^k) as x->a.
1/(1-x) = 1 + x + x^2 + ⋯
ln(1+x) = Σ(-1)^{n+1} x^n/n

Integration

Chain rule: $\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}$
Integration by substitution or u-sub. $\int u(x) du(x) = \int u du$. Need to change the limits of integration for definite integrals.
Integration by parts: $\int u dv = uv - \int v du$. For definite integrals the product is evaluated between the limits. Useful for inverse functions and logs.
Cavalieri’s principle: solids with equal cross-sectional areas have equal volume.

$\textrm{d}e^x = e^x$
Eigenfunction of differentiation: $e^x$ is unchanged by differentiation.
Continuous compounding: always grow by the current amount.

Slope at 0, or eigenvalue C: $a^x$ = $e^{Cx}$.

$e^x$ must have slope 1 at 0. Consider a linear approximation at $x=\frac1n$. As $n\to\infty, e^{1/n} = 1 + \frac1n \Rightarrow e = (1+\frac1n)^n$. More generally, $\displaystyle e^z = \lim_{n\to\infty} \left(1+\frac{z}n\right)^n$.

The slope of $a^x$ at $x$ is $a^x$ times its slope at 0:
\[\frac{d}{dx} a^x = \lim_{h\to0} \frac{a^{x+h} - a^x}h = a^x \lim_{h\to0} \frac{a^h-1}h\]

Intercept at 0: $Ce^x$ is unchanged.

Shifting along x is equivalent to scaling y. It determines the initial amount at x=0. To be unchanged, the slope at 0 must equal the intercept at 0, so $e^x+C$ is not an eigenfunction.

Taylor series: $e^x = \sum \frac{x^n}{n!}$

Can derive the coefficients from $\textrm{d}e^x = e^x$ and $e^0 = 1$.

Gamma function generalizes the factorial

$\Gamma(x) = \int_0^\infty t^{x-1} \exp(-t) dt$
$n! = \Gamma(n+1)$
$\Gamma(1/2) = \sqrt\pi$

Fractional calculus and the differintegral

$D^{-1} f = \int_0^x f(t) dt$
$D^{-n} f = \frac1{(n-1)!}\int_0^x (x-t)^{n-1} f(t) dt = \frac1{\Gamma(n)}\int_0^x (x-t)^{n-1} f(t) dt$ from the Cauchy formula for repeated integration
$D^n x^a = \frac{a!}{(a-n)!} x^{a-n}$
$D^{1/2} x^a = \frac{a!}{(a-1/2)!} x^{a-1/2}$
For more general

Vector calculus

Divergence ∇·F is the volume density of outward flux at each point.
Curl ∇×F is the rate of rotation at each point in F.
- (∇×F)·u = lim_{A->0} 1/|A| ∮ F·dr for a line integral around an area A.
- A conservative (path-independent) vector space has no curl.
Divergence theorem or Gauss’s theorem. The integral of the divergence over a volume V is the flux through its surface S: ∫∫∫ ∇·F dV = Φ_S = ∫∫ F∙dS.
- Green’s identities is the analogue of integration by parts.
Curl theorem or Stokes’ theorem. The integral of the curl over a surface S is the integral of the field over its boundary B: ∫∫ (∇×F)·dS = ∮F·dB.
- Green’s theorem.
Helmholtz decomposition theorem or the fundamental theorem of vector calculus. A smooth vector field decomposes into an irrotational field and a solenoidal (divergence-free) field.

1730. Generating function represents an sequence as the coefficients of a formal power series.

https://en.wikipedia.org/wiki/Generating_function#See_also

Nonstandard analysis uses infinitesimal numbers.

Signal processing

Harmonic analysis decomposes functions into simpler functions.

A compact group is a compact topological space.

Many results of finite group representation theory are proved by averaging over the group. For locally compact groups, we can generalize these results to infinite groups by defining integration based on the Haar measure.
Groups of orthogonal matrices.

Fourier series

Continuous signal of period T to discrete harmonics $n/T$.
$c_n = \frac1T \int_{-T/2}^{T/2} f(x) \exp(-2\pi i \frac{n}T x) dx$
$f(x) = \sum_{-\infty}^{\infty} c_n \exp(2\pi i \frac{n}T x)$

Continuous Fourier transform: limit as $T\to\infty, n/T \to\omega$

Continuous, rapidly decreasing signal of infinite length.
$f(\omega) = \int_{-\infty}^\infty f(x) \exp(-2\pi i \omega x) dx$
$f(x) = \int_{-\infty}^\infty f(\omega) \exp(2\pi i \omega x) d\omega$

Discrete-time Fourier transform (DTFT). Period $2\pi$ sampled at frequency $\omega = 1/2\pi$.

Maps between discrete time samples of infinite length and a continuous, periodic function of frequency.
$X(\omega) = \sum_{-\infty}^\infty x[n] e^{-i\omega n}$
$x[n] = \frac1{2\pi} \int_{-\pi}^{\pi} X(\omega) e^{i\omega n} d\omega$

Discrete Fourier transform (DFT) is a sampled version.

Finite-length discrete signal and a discrete frequency spectrum.
Can be computed via Fast Fourier transform (FFT).
$X[k] = \sum_0^{n-1} x[n] \exp(-2\pi i \frac{n}N k)$
Inverse $x[n] = \frac1N \sum_0^{N-1} X[k] \exp(2\pi i \frac{k}N n)$

1940. Nyquist-Shannon sampling theorem

Discrete-time Fourier transform (DTFT) takes uniform samples
Nyquist rate is twice the highest frequency (bandwidth) of a signal.
Aliasing is overlap of frequency components. Occurs iff the sample rate is below the Nyquist rate.
- Stroboscopic effect or wagon-wheel effect
https://en.wikipedia.org/wiki/Aliasing

Laplace transform: continuous-time signal to the complex s-domain. $s = i\omega$

$\mathcal{L}(s) = \int_0^\infty f(t) e^{-st} dt$

z-transform: discrete-time signal to the complex z-plane.

$X(z) = \sum_{-\infty}^\infty x[n] z^{-n}$
$x[n] = \frac1{2\pi} \int_{-\pi}^\pi X(e^{i\omega}) e^{i\omega n} d\omega$

Linear time-invariant (LTI) systems.

Filters

An impulse is a Dirac delta function. It is constant in frequency space, so the impulse response fully defines an LTI system.
- finite impulse response (FIR) filter vs. infinite impulse response (IIR).
bounded-input, bounded-output (BIBO) stability
- Impulse response is absolutely integrable (finite L1 norm)
In a causal system, an output only depends on past inputs.
- A causal transfer function uniquely factors into an all-pass and a minimum phase system.
Fourier transform to a complex-valued function of frequency.
Laplace transform to the complex-valued frequency domain or s-domain. Decomposes a function into its moments. Fourier is the line s = iw.
Discrete time: z-transform. Wiener filter.
A window function is a low-pass filter. High-pass and band-pass also exist.
- The sinc function is the Fourier transform of a boxcar.
- A time-domain sinc function implements a brick-wall low-pass filter.
Gibbs phenomenon: any partial Fourier series of a function will overshoot by about 9% around a discontinuity.
- The Heaviside step function is discontinuous, so the step response will have ringing artifacts.
Compression or decimation: low-pass filter, then keep every nth sample.
A linear phase filter if the phase response is linear in frequency. All frequency components are shifted by the same group delay (the slope), so there is no relative phase distortion.
- In discrete time, a FIR filter with symmetric or anti-symmetric coefficients is linear phase.
All-pass filter: equal gain but changes phase relationships.
Comb filter: add a delayed version of the signal to itself, creating a toothed frequency response.
A system is minimum-phase if it and its inverse are causal and stable.

https://en.wikipedia.org/wiki/Flanging
https://en.wikipedia.org/wiki/Downsampling_(signal_processing)

An analytic signal is a complex-valued function without negative frequency components.

The Fourier transform of a real-valued function has Hermitian symmetry, so the negative frequency components can be discarded with no loss of information.
The Hilbert function relates the real and imaginary parts.
A phasor is an analytic signal with time-invariant amplitude, phase, and frequency.

Group delay and phase delay

Control theory

1868 Early control theory: On governors by Maxwell.
1877 Routh–Hurwitz theorem and the Routh-Hurwitz stability criterion: the characteristic polynomial of the differential equations of a stable linear system has roots limited to the left half plane (negative eigenvalues).
https://en.wikipedia.org/wiki/Control_theory

Differential geometry

Differential geometry is the study of calculus on differentiable manifolds.

A differentiable manifold has unambiguous global differentiation.
Extends differentiation to spaces without global coordinate systems.
Transition maps of coordinates from one chart to another are differentiable.

A metric space is a set with a metric or distance function which satisfies identity, positivity, symmetry, and triangle inequality.

A metric space induces a topology, but not every topological space is metrizable.

A manifold is a topological space that locally resembles Euclidean space. Each neighborhood is homeomorphic to R^n or C^n.

A knot is an embedding of a circle in R^3. Two knots are equivalent if there is an ambient isotopy, a continuous distortion of an ambient space that does not involve cutting the string or passing the string through itself.
A chart is a homeomorphism from an open subset of a topological space to an open subset of Euclidean space.
An atlas is a collection of charts that cover the manifold.
A fiber bundle is a space B which is locally a product space. It has a continuous surjective projection or submersion, π : E → B, which locally behaves like a projection from B × F to B.
A vector bundle over X associates or attaches every point x in a space with a space V(x), such that the spaces V(x) fit together as a space.

The tangent space T_x M of a manifold M at a point x generalizes tangent line and tangent plane.

The tangent bundle is a manifold TM of tangent spaces for all points on M: all points (x, T_x M).
For a smooth map f: M -> N, the pushforward or differential df is a linear approximation from T_x M to T_{f(x)} N. It generalizes the total derivative.
The cotangent space T_x* M is the dual space of T_x M.

An affine connection connects tangent spaces on a manifold.

Parallel transport moves vectors of the manifold along curves so that they stay parallel with respect to the connection.

1873. A Lie group is a continuous group where group multiplication and inverse is differentiable, forming a differentiable manifold. Many are compact.

Circle group (complex unit circle) exhibits continuous symmetry.
Classical groups
- general linear group GL(n): group of nxn invertible matrices
  - orthogonal group O(n): nxn orthogonal matrices. Algebraic group.
  - unitary group U(n): complex analogue of orthogonal
- special linear group SL(n): group of nxn matrices with determinant 1. Forms an algebraic subvariety of GL since the determinanat is a polynomial.
  - special orthogonal group SO(n) or rotation group: nxn orthogonal matrices of determinant 1.
  - Lorentz group O(3, 1) is the group of all Lorentz transformations of Minkowski spacetime.
  - special unitary group SU(n): nxn unitary matrices with determinant 1
- Symplectic group Sp(2n) is the linear transformations of a symplectic vector space. Group of 2nx2n symplectic matrices, which satisfy M^T Ω M = Ω, where Ω is the block matrix $[0 I_n -I_n 0]$.
Linear algebraic groups or affine group schemes generalize Lie groups beyond R and C using algebraic geometry.

A symplectic manifold is a smooth manifold with a symplectic form ω, which is a closed nondegenerate differential 2-form.

A Kähler manifold is a complex manifold which is also Riemannian and symplectic. Hermitian Yang–Mills connections and Kähler–Einstein metrics. David van Dantzig 1930.

A Riemannian manifold is a real smooth manifold M equipped with a positive-definite inner product or Riemannian metric tensor g_p on the tangent space T_pM at each point p. A Hermitian manifold is the complex analogue.

Riemann curvature tensor is a tensor field which measures the failure of the second covariant derivatives to commute. Zero curvature iff it is flat locally isometric to Euclidean space.

Conformal transformations preserve angles or equivalently the inner product up to a scale factor.

Riemann mapping theorem states that any simply connected open subset of complex plane has a bijective holomorphic or conformal mapping onto the open unit disk.

Uniformization theorem: every simply connected Riemann surface is conformally equivalent to the open unit disk, the complex plane, or the Riemann sphere.

Geometrization conjecture says that every 3-manifold is locally equivalent to one of eight types of geometry. As a corollary, the Poincaré Conjecture states that every closed 3-manifold with with the same topology as a sphere is a geometric sphere. Conjectured by William Thurston in the 1980s and proven by Grigori Perelman in 2003.

Brouwer fixed-point theorem (1911): every continuous function from a closed disk to itself has at least one fixed point.

Sperner’s lemma: given a triangle where the vertices have distinct colors is subtriangulated, and given a Sperner coloring, where the added vertices along any original edge must have one of the two original colors on the ends, then there must be an odd number of rainbow triangles with three different colors.

Banach fixed-point theorem (1922): a contraction mapping of a complete metric space has a unique fixed point which can be found by iterating the mapping.

Lefschetz fixed-point theorem (1926) counts the fixed points of a continuous mapping from a compact topological space X to itself by means of traces of the induced mappings on the homology groups of X. Leads to the Poincaré–Hopf theorem. Nielsen theory says that any map f has at least N(f) fixed points, where N(f) is the Nielsen number.

A holomorphic function is complex differentiable in a neighbourhood of each point.

Cauchy integral theorem. Any simple closed contour of a holomorphic function integrates to 0.
A meromorphic function is holomorphic on an open subset D of the complex plane except for a set of isolated poles. It can be expressed as a ratio of two holomorphic functions.
A complex manifold has an atlas of charts to the open unit disc in C^n with holomorphic transition maps. Locally it looks like the complex plane.
- A Riemann surface is a connected one-dimensional complex manifold, for example graphs of multivalued functions like √z or log(z).
  - A modular curve is a Riemann surface or corresponding algebraic curve. Quotient of the complex upper half-plane H by action of a congruence subgroup Γ of the modular group of integral 2×2 matrices SL(2, Z).
  - The points of a modular curve parametrize isomorphism classes of elliptic curves.
An elliptic function is a meromorphic function that satisfies f(z + ω_1) = f(z) = f(z + ω_2).
- It is doubly periodic (periodic over the complex plane).
- Inverse of an elliptic integral $f(x) = \int_c^x R(t, \sqrt{P(t)}) dt$
The modular group is the projective special linear group PSL(2, Z) of 2×2 matrices with integer coefficients and determinant ad-bc=1, which represent transformations z -> (az+b) / (cz+d).
A modular form is an homomorphic function on the upper half-plane, bounded as z → i∞, where f((az+b) / (cz+d)) = (cz+d)^k f(z). Each modular form has a Galois representation.

https://en.wikipedia.org/wiki/Hairy_ball_theorem
https://en.wikipedia.org/wiki/Template:Manifolds

Optimization

Misc

https://en.wikipedia.org/wiki/Mathematics_Subject_Classification
https://en.wikipedia.org/wiki/Fields_Medal
https://haimgaifman.files.wordpress.com/2016/07/22odel-to-kleene.pdf
https://web.archive.org/web/2015/http://www.columbia.edu/~hg17/Inc07-chap0.pdf
https://web.archive.org/web/2015/http://www.columbia.edu/~hg17/Diagonal-Cantor-Goedel-05.pdf

https://www.scottaaronson.com/democritus/lec3.html
https://www.scottaaronson.com/democritus/lec4.html

Weber
Dedekind
Abraham Robinson
The Nicolas Bourbaki group publishes the Elements of Mathematics (1934).
https://en.wikipedia.org/wiki/Foundations_of_mathematics
https://en.wikipedia.org/wiki/Second-order_logic
https://en.wikipedia.org/wiki/Second-order_propositional_logic

Contents